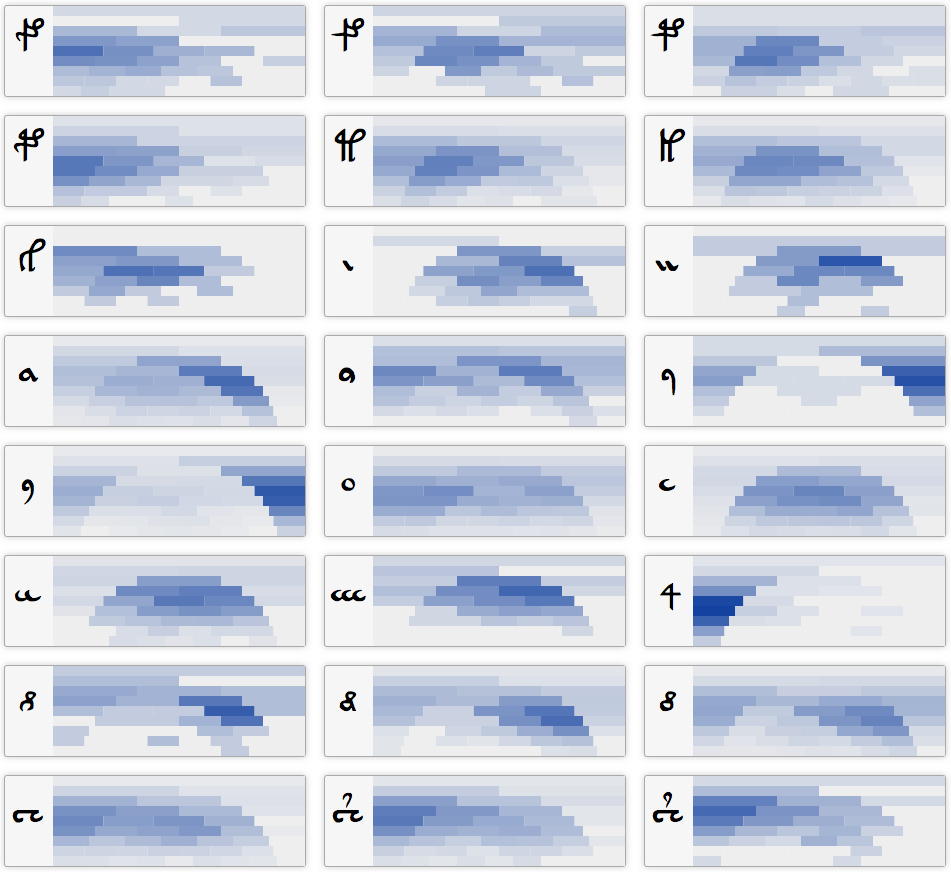

These charts show where glyphs appear within words in the Voynich MS. Rows represent all words of a particular length, from words of length one at the top to nine at the bottom. Darker blue indicates more appearances in that position.


These charts show the frequency of glyphs in each position within unique words. Glyphs have been ordered according to the relation order calculated in the study of related Voynich MS glyphs.
So for example, imagine we had the input text "I am a tall guy". The chart for the letter "a" would have a light blue rectangle on the first row, because 50% of 1-letter long words are "a". The second row would by 100% blue on the left side, and 100% white on the right side, because there is only one 2-letter word and it starts with an "a". The third row would be entirely white, because there is only one 3-letter word and it doesn't contain the letter "a". The fourth row would be blue in the second rectangle because of the "a" in "tall".
These charts, therefore, reveal the distribution of glyphs within words of all lengths simultaneously. This at-a-glance overview makes it possible to compare distributions easily, which is especially helpful when comparing glyphs.
One of the most obvious features of the charts is that many display a "dome" shape. This suggests a division of words into two regions: the outside, i.e. the first and last glyphs; and the inside, i.e. the middle.
The glyphs 9, o, and c display this feature clearly:

Where 9 is an outside glyph, o is a mixture, and c is an inside glyph.
There are some very clearly single-position characters, too. 4 always comes at the start, a is penultimate, and M comes at the end. Some also seem to be hybrids, such as 8 which is usually either the first or the penultimate glyph.
One interesting feature that the graphs reveal is a potential difference between the f u j g glyphs. The f g glyphs, which have hooks on the leftward facing stems, are distributed fairly evenly between the first and second characters on average. On the other hand, u j, which don't have the hook, are much more inclined to come only second in a word.
The dome shape of many charts may indicate some relationship with Stolfi's proposed crust-and-core idea. Stolfi classed k g h u K G H U as core glyphs, 1 2 C as mantle glyphs, and 8 e y s N | i p * as crust glyphs. The charts above do, however, indicate that the reality is more complex than this idea would suggest.
Here is a sample of what the distribution patterns look like for glyphs when the first and last glyphs of a word are excluded:

Two other sorting schemes were tried for presenting the data: frequency, and average position. Surprisingly, average position did not yield the most interesting results, probably because it ignores the outside-inside distinction. The fact that the relation order, based on previous research, was most useful sorting scheme bolsters the validity or at least the usefulness of that research.
These were the schemes used for sorting:
| Frequency | o 9 a c 1 e 8 h y k 4 m 2 C 7 s n p K g H A j 3 z 5 ( d i f u M * Z % N J 6 I x + W G Y E ! t P |
| Position | 4 g k j 2 f h o 1 % 3 + W ! 5 G K u J E c I A t d H i 8 e C s 7 6 a x z Y Z y ( M P 9 N * m n p |
| Group | f u j g k h W i I a A ( 9 o c C d 4 6 7 8 1 2 3 5 % + ! K H J G t s E * e y x m n z P p M Z N Y |
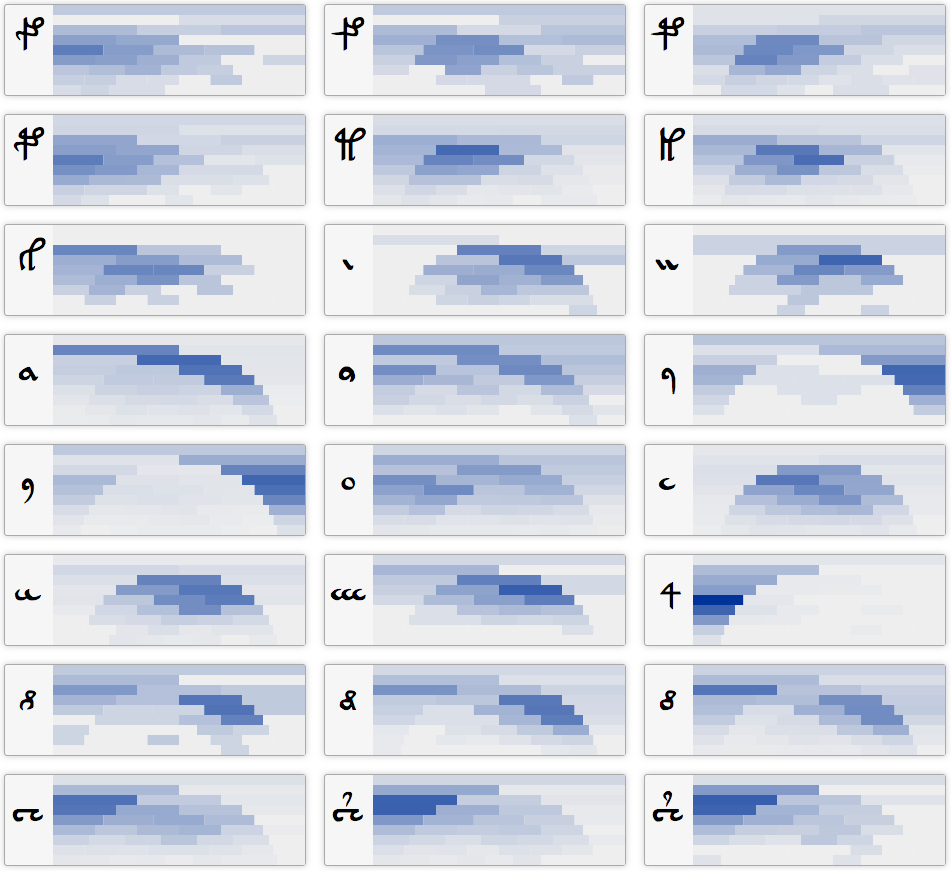
Another alternative that was explored was using all words from the manuscript rather than unique words. In other words, for the results at the top of this page all words were filtered so that they only occurred once, bringing the length of the manuscript down from 40,716 to 9,858 words. The alternative of using all words did not, however, make much difference to the results:


The first row shows the unique-words-only results, and the second row shows the results from the normal version of the manuscript. One of the main differences between the two is that there is far less bias towards the one and two glyph words in the unique version, at least in part because there are far fewer possible combinations of one and two glyph words than there are for three and above.
Here are all of the results for all words:
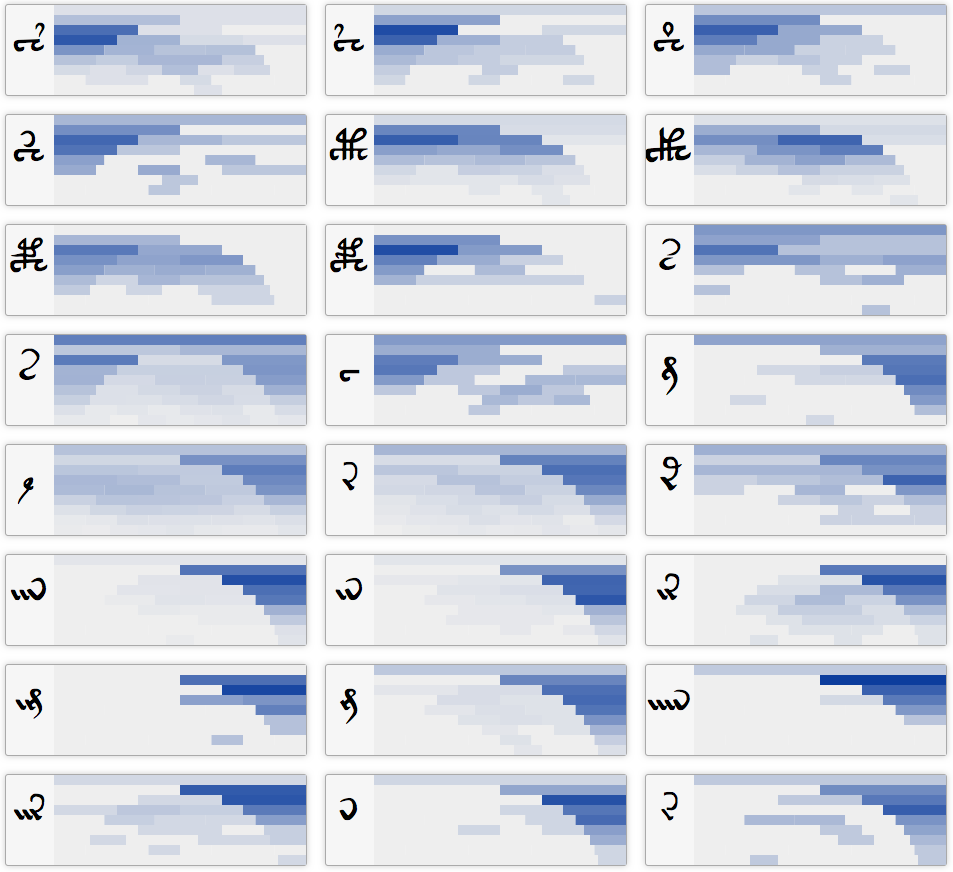
The maximum word length in the transcription used is 12, but the graphs above only plot up to 9. This is because the frequency drastically falls off after about 6 or 7:
| Letters | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | 1971 | 5559 | 9372 | 9683 | 8203 | 4113 | 1410 | 309 | 77 | 15 | 1 | 3 |
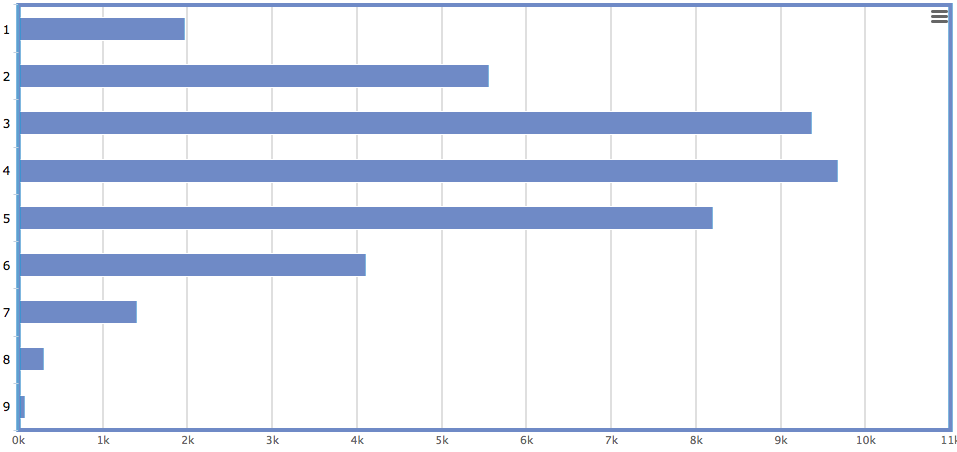
Therefore, the results from words of of greater than length 9 would barely show up in the charts. Indeed, there are so few words over 9 glyphs long that they can just be listed:
Apart from oooooooooeay and the okc / ohc words, they seem at least superficially normal.
Glen Claston's Voynich 101 transcription was used for the source of this analysis. A short python program was used to parse the data, which was then plotted using a CoffeeScript program and d3.js. The files and data are available:
Claston's transcription was chosen because of the high degree of granularity regarding the glyphs. No other transcription comes close to providing the same amount of detail. Only the 48 most common glyphs were used in this analysis. 48 was chosen because it would have been difficult to display much more data in an easy to consume manner.
The charts are licensed under CC by-sa 4.0. The source code and data linked above are licensed under the Apache License 2.0.
The voynich-101.woff font used in this document, and in the chart, was prepared for me by David P. Kendal from the original public domain VOYNICH.TTF font by Glen Claston. I am also very grateful for Claston's work on the font and transcription, and his commitment to place the font in the public domain. Credit does not imply approval or otherwise of this article, excepting that David P. Kendal requires that I mention his explicit approval of my work.
Sean B. Palmer, June to August 2014